The exp() function allows you to raise Euler’s Number \(e\) (the base of the natural logarithm) to a higher power and get the output, where the argument is the exponent:
exp(number) number.exp()
\(e\) approximately equals 2.718281828459045.
Good to know: exp(n) is equivalent to e^n. See e (Constant) for more.
Viewed another way, the exp() function helps you find the argument (mathematical term) in a natural logarithm.
In other words, exp() accepts \(x\) as an argument (programming term) and returns \(y\), where:
For reference, here are the named components of a logarithm:
\(\log_{base} argument = exponent\)Learn more about natural logarithms here:
Example Formulas
exp(2) /* Output: 7.389056098931 */
5.exp() /* Output: 148.413159102577 */
e ^ 5 /* Output: 148.413159102577 */
exp(ln(5)) /* Output: 5 */
5.ln().exp() /* Output 5 */
Example Database
Using exp(), we can write a Notion formula that models continuous growth of a starting population by a certain percentage each year over a certain number of years.
This example is also used in the article on Euler’s Constant (e); its use here demonstrates how exp(n) is equivalent to e^n.
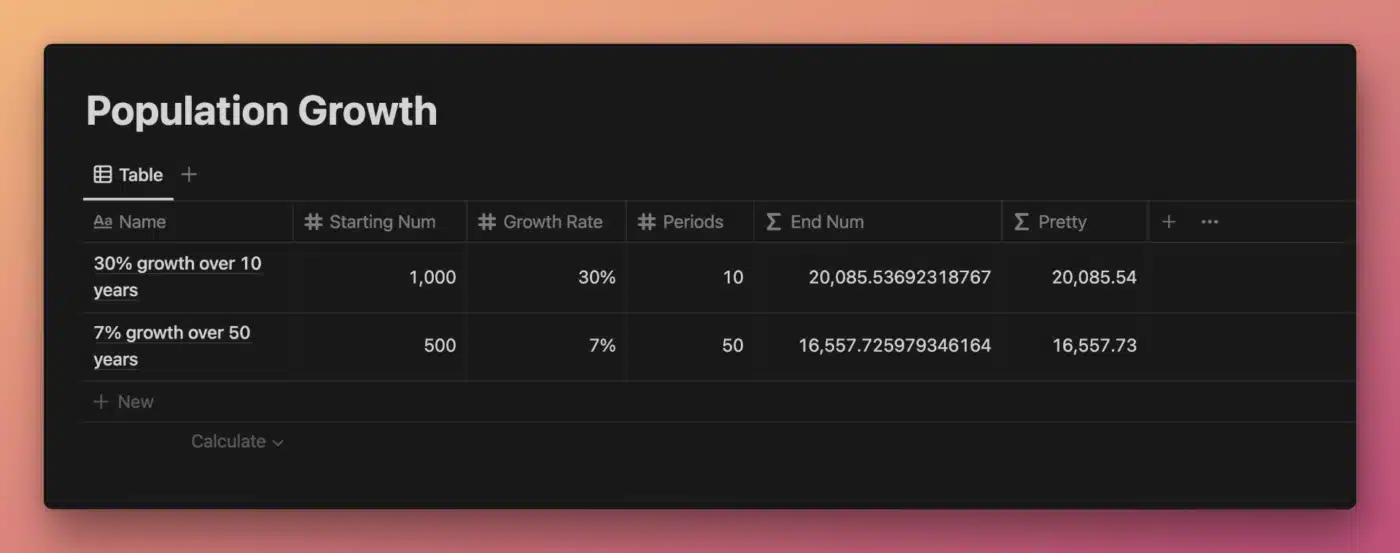
View and Duplicate Database

“End Num” Property Formula
prop("Starting Num") *
exp(
prop("Growth Rate") *
prop("Periods")
)
As stated in the Euler’s Constant (e) article, continuous growth of a starting number \(n\) can be expressed as:
\(n * e^{(rate \ of \ growth \ * \ number \ of \ time \ periods)}\)Here, we simply use the exp() function, passing prop("Growth Rate") * prop("Periods") as the argument.
We then multiply it by our starting number, passed via prop("Starting Num").
Other formula components used in this example:




